Конкурс Сазнали на семинару применили у пракси 2019

Пријава на конкурс:

ПРОЈЕКАТ САТ

Опис пројекта

Тема пројекта је Сат. У складу са темом у наставку је представљен планиран начин реализације пројекта.

Циљ пројекта:

Подстицање креативности ученика и нових начина стицања знања самосталним истраживањем и коришћењем нових технологија. Развијање међупредметних компетенција уз повезивање стечених знања са свакодневним животом.

Исходи:

Ученик ће бити у стању да:

препозна и опише разлику између различитих типова сатова
препозна и опише разлику између временских зона
користи информационе технологије у решавању проблема
креира сат у Геогебри
нацрта мрежу ромбикосидодекаедра у Геогебри
истражи кроз Wolfram alpha изглед ромбикосидодекаедра
креира слике у PicsArt-у
направи QR Kôd
селектује битне информације
конструише правилне многоуглове
максимално искористи расположиви материјал за рад
креира прегледну ППТ
повеже тему са другим предметима и да сагледа ширу слику у оквиру просторно- временског контекста;
успешно сарађује са наставницима, ученицима и локалном заједницом.
саслуша и уважи туђе мишљење
аргументовано брани свој став

План пројекта

Пројекат се реализује у другом полугодишту, у месецу марту, априлу и мају, оквирно два час недељно.

недеља: Анализа задатог проблема и одређивање циља пројекта.
недеља: Формирање група према афинитетима ученика, уз подршку од стране наставника како би се постигла уравнотеженост група. У сваком одељењу којем предајем формирана је група од 5 ученика. Укупно је 25 ученика од петог до осмог разреда.
недеља: Избор адекватног решења и корелација са другим предметима (српски језик, физика, техника и технологије, информатика, географија). Планирање тока рада по фазама.
4. до 8. недеље: Рад на реализацији пројекта, прикупљање потребних информација и анализа истих од стране ученика уз консултацију са наставником.
9. и недеља: Креирање крајњег продукт рада.
11. недеља: Презентовање резултата рада.
недеља: Оцењивање и вредновање резултата у сарадњи ученика и наставника.

Активности ученика и наставника, начини презентовања пројекта

Активности наставника:

Предлаже циљ и тему пројекта.
Формира групе у сарадњи са ученицима.
Прати, пружа подршку и усмерава ученике у раду.
Подстиче ученике на стваралачко истраживање.
Подстиче сарадњу и тимски рад међу ученицима.
Помаже ученицима у превазилажењу тешкоћа и савладавању проблема.
Заједно са ученицима вреднује резултате.
Пружа помоћ при остваривању видљивости резултата пројекта.

Подстиче ученике да изкажу своје мишљење и ставове.

Подстиче ученике да вежбају јавни наступ.
Помаже ученицима да уоче да је математика свуда око нас.

Активности ученика:

Планирају фазе и ток реализације;
Прикупљају информације, материјале, врше анализу;
Креирају крајњи продукт;
Презентују резултате;
Учествују у вредновању резултата.

Праћење и вредновање пројекта

Дискусија

Наставник дискутује са ученицима о свим недоумицама, страховима, нејасноћама, очекивањима и идејама које уносе у заједнички пројекат на почетку приликом представљања модела пројектне наставе који ће користити у даљем раду, али и у току самог процеса израде пројекта зарад превазилажења евентуалних проблема. Такође, дискусија је била заступљена и као један од модела завршних активности ради изношења сугестија за унапређивање будућег рада;

Рефлексија

По завршетку сваке од фаза рада ученици су позвани да рефлектују сопствени и групни рад у односу на различите карактеристике: задовољство, продуктивност, услови рада.

Евалуација

Путем Гугл упитника- ученици ће попунити е-упитник креиран од стране наставника, а на основу претходно договорених сегмената рада. Предложено је да упитник буде састављен у форми скале процене уз простор за дописивање додатних коментара и идеја.

Скала процене из угла ученика:

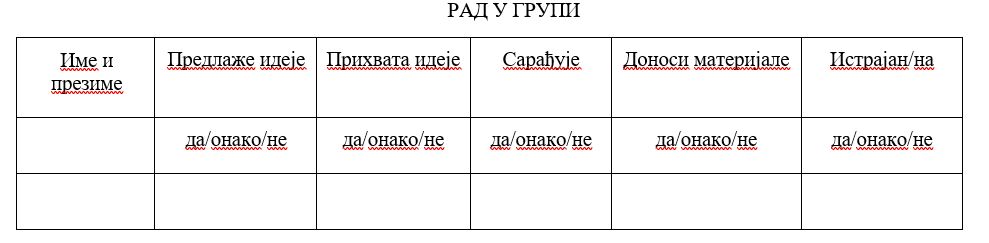
Наставничка евалуација

Наставник је креирао сопствену табелу за праћење и вредновање процеса на индивидуалном и групном нивоу. Утиске и процену ће поделити са ученицима по завршетку.

Скала процене из угла наставника (описно):

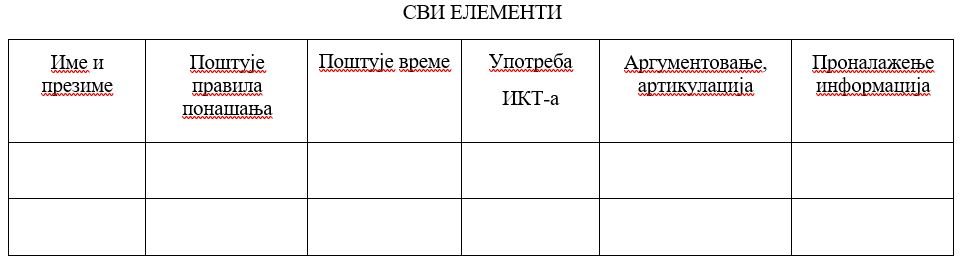
Разрада пројекта

У корелацији са српским језиком ученици су истраживали занимљивости у вези са временом и представили своја размишљања о сату. Из физике ученици уче осцилације и таласе који су кључни за рад сата са клатном, као и појам времена и његове мерне јединице. У петом разреду из географије обрађује се ротација Земље око осе што нам помаже да разумемо све 24 временске зоне у свету и искористимо то знање у нашем пројекту.

Први сатови

Поред потребе за већим временским јединицама од дана, јавила се потреба и за мањим као што су сат, минут и секунда. Секунда спада у 7 основних мерних јединица СИ система. Са овом потребом почео је развој уређаја за мерење времена.

Сат са клатном

Године 1657. сатови су додатно усавршени проналаском сата с клатном. Ова идеја је изворно потицала од Галилеја који је желео да искористи њихајуће клатно за покретање сатног механизма. Међутим, обично се Кристијан Хајгенс сматра за проналазача сата са клатном. По његовим прорачунима израђен је први такав сат.

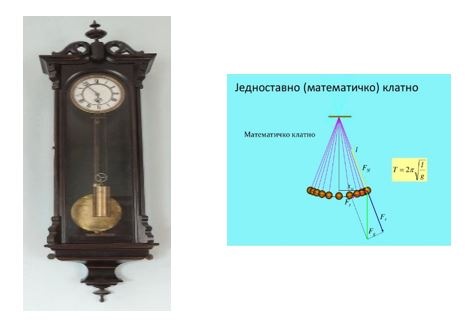
Свако кретање које се понавља по једнаким временским интервалима назива се периодично, ако се кретање одвија стално по истој путањи око равнотежног положаја у два смера, назива се осцилаторно. Код часовника са клатном су главни делови покретач, регулатор, преносни механизам и показивач. Покретач је тег, односно сила теже. Регулатор је клатно. Показивач је бројчаник са казаљкама. Тег виси о једној струни намотаној на један котур који има заједничку осовину са секундним зупчаником. Падајући тег одмотава струну и окрће секундни точак. Када се клатно заклати, оно по својој особини осцилује у једнаким временским размацима између два амплитудна положаја. Ово време се назива период осциловања и код клатна зависи од његове дужине. Дужина клатна се може подесити тако да период осциловања буде 1 s, тј. да клатно изврши једну осцилацију у једној секунди. У том случају дужина клатна је отприлике 1 m. У истом ритму са клатном се клацка и котва која пропусти један зубац секундног точка, а секундна казаљка откуца једну секунду. С друге стране удари зубца у котву подстичу клатно да не смањи своју амплитуду и не стане услед трења у механизму и услед отпора ваздуха. Обртање секундног точка се преко низа зупчаника преноси на минутни и часовни точак на чијим се осовинама налазе казаљке које показују минуте и часове. Промене у температури и атмосферском притиску доводе до промене дужине клатна па се мора водити рачуна о условима у којима се налази часовник јер ће се у супротном променити период осциловања и више сат неће показивати тачно време.

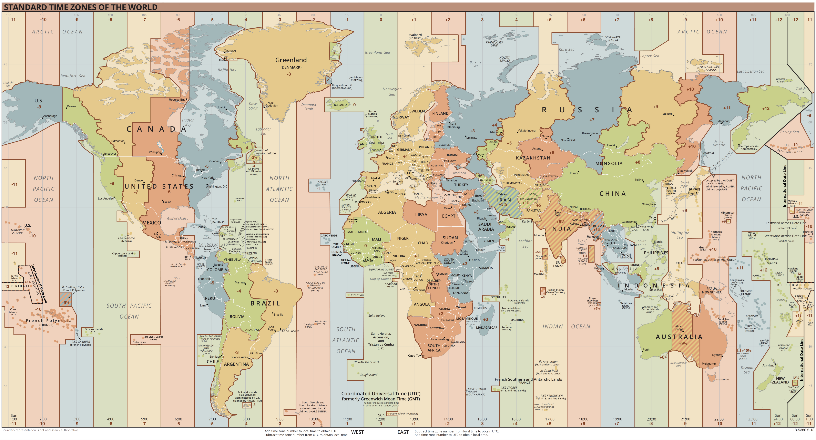
Временске зоне

Ротација је кружно кретање Земље око своје осе. Земља направи пун круг за један дан, тачније 23,9344 часа. Окретање земље врши се од запада ка истоку. Земљина ротација доводи до бројних последица које условљавају разноврсне појаве: смена обданице и ноћи, привидно дневно кретање Сунца, плима и осека, часовне зоне. Договорено је у Вашингтону 1892. године, на конферецији у којој је учествовало 25 држава, да се Земљина кугла подели на 24 временска појаса, тако да сва места унутар једне зоне имају исто зонално време. Као почетни меридијан узет је меридијан који пролази кроз астрономску опсерваторију у Гриничу код Лондона. По један сат додаје се приликом преласка меридијана у правцу истока, док се по један сат одузима приликом преласка меридијана у правцу запада. На слици испод приказане су стандарне временске зоне на Земљи. Зато се често користи средње време по Гриничу (GTM). Све остале временске зоне се координишу у односу на ову почетну вредност.

Математички појмови и софтверски алати

С обзиром на то да постоје тачно 24 временске зоне идеја је да се направи сат који ће приказивати тачно време у свим зонама у истом тренутку. Детаљном анализом одлучено је да модел буде једно од 13 Архимедових полиедара- ромбикосидодекаедар.

Полиеадар је тродимензионално рогљасто геометријско тело ограничено полигонима (странама полиедра), тако да сваку ивицу деле тачно два полигона. Пресек две суседне стране полиедра је ивица, а тачка у којој се секу суседне ивице полиедра је теме. Дијагонала полиедра представља дуж која спаја два његова темена, а да при томе не припада ниједној његовој страни. У случају полиедра, полиедарска површ је затворен скуп полигона и дели простор на спољашњи и унутрашњи, а тек заједно са унутрашњим простором чини полиедар.

Архимедова тела су конвексни полиедри и спадају у полуправилне полиедре прве врсте – имају подударна темена, све ивице су једнаке, а странице су им правилни полигони, али те странице нису подударне. Око било ког Архимедовог полиедра се може описати сфера, која садржи сва његова темена и међусфера, која додирује средине свих његових ивица.

Wolfram alpha – детаљни опис ромбикосидодекаедра

Детаљни опис ромбикосидодекаедра добили смо користећи Wolfram alpha-у. Упит се креира уносом одговарајућег математичког појма и задатим карактеристикама. У овом случају то је ромбикосидодекаедар са ивицом дужине 9cm. Одговарајућа адреса и резултати упита дају детаљни опис ромбикосидодекаедра који је описан испод. Ромбикосидодекаедар је састављен од 12 правилних петоуглова, 20 једнакостраничних троуглова и 30 квадрата. Има 120 ивица и 62 стране.

rhombicosidodecahedron, minimal edge length = 5

https://www.wolframalpha.com/input/?i=rhombicosidodecahedron,+minimal+edge+length+%3D+9

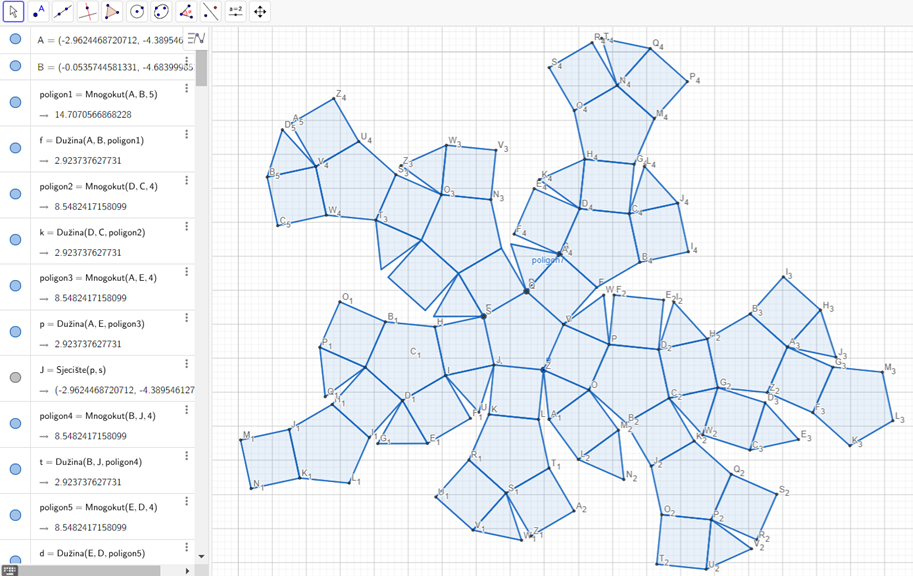
Geogebra – мрежа ромбикосидодекаедра са задатим параметрима

Скуп свих полигона, који ограничавају полиедар, назива се полиедарска површ, док исти скуп полигона, развијених у једној равни, представља мрежу полиедра. Приказ мреже ромбикосидодекаедра помогао нам је при конструкцији мреже модела:

Geogebra android – Мобилна апликација

Коришћење Геогебра мобилне апликације за једноставно дефинисање геометријских фигура и обнављање градива.

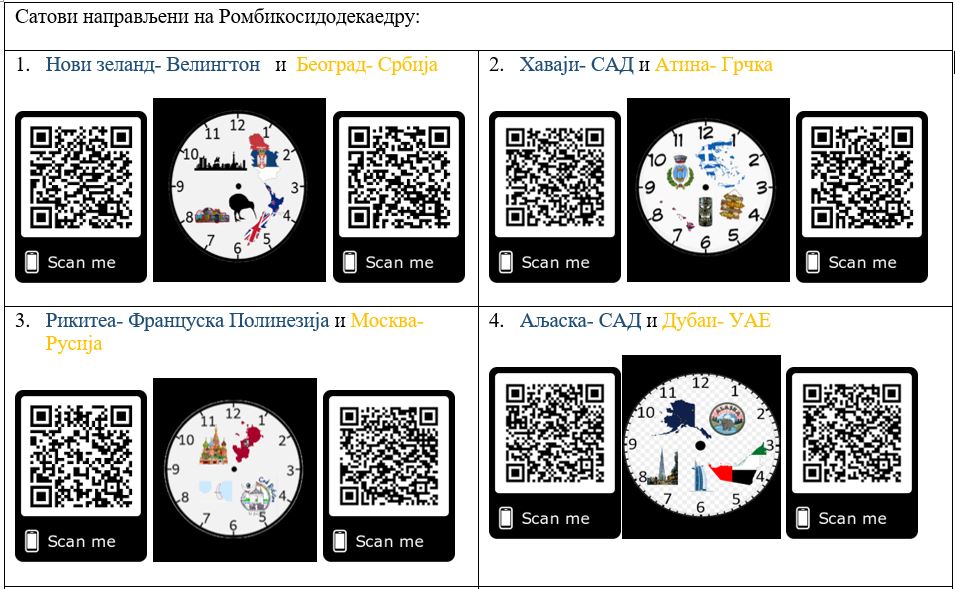
PicsArt- мобилна апликација за уређивање фотографија и прављење колажа. PocsArt нам је омогућио да на једноставан начин креирамо налепнице за сатове. За сваки од 12 сатова креирана је посебна налепница. На свакој налепници представљена су главна обележја два изабрана града који су представници одговарајуће временске зоне.

QR Kôd- дводимензиони матрични бар-код који омогућава брже читање и чување веће количине информација. QR Kôd је коришћен за добијање више информација о занимљивостима града који је представник временске зоне. Због уштеде места и доступности што више информација о одређеном граду одлучили смо се за креирање QR Kôd-а који смо одштампали у виду налепнице и залепили на ромбикосидодекаедру поред сата на који се односи.

3D бојанка- приказ мреже ромбикосидодекаедра са налепницама сатова

Етапе израде макете и радионица- прављење ромбикосидодекаедра од сламчица

На жутом хамеру је конструисана мрежа ромбикосидодекаедра по угледу на мрежу која је креирана у Геогебри. Затим је залепљено 12 дискова на странама петоугла, а са одговарајуће доње стране су излепљени механизми за сатове. На сваком диску су залепљене креиране налепнице и стављене казаљке. Сваки сат је навијен по тачном времену у зони којој одговара. QR Kôd-ови су излепљени поред сата чије карактеристике града садрже.

Организована је и радионица на којој је направљен ромбикосидодекаедар од сламчица.

Задаци у вези сата:

Колико пута у току 12 часова неко мисли на нас?

Од давнина се верује да неко мисли на нас када су казаљке поклопљене. Тим проблемом бавили смо се у овом пројекту и до тачног одговора дошли смо математичким путем.

Сатна казаљка креће се 12 пута спорије од минутне. Она опише пун круг за 12 часова, а минутна за 1 час. Ако у 12 часова обе казаљке крећу од броја 12. После једног часа сатна казаљка је прешла једну дванаестину пуног круга, а минутна је прешла пун круг и поново је на броју 12. У току следећих неколико минута доћи ће први пут до поклапања две казаљке између бројева 1 и 2. Пошто минутна казаљка прође више од пуног круга, а сатна пређе иза броја 2, доћи ће до њиховог новог поклапања између броја 2 и 3. До последњег поклапања пре 12 часова доћи ће између бројева 10 и 11. После броја 11 и све до броја 1 казаљке ће се поклопити још само једном и то у броју 12. Па закључујемо да ће за 12 часова доћи до поклапања казаљки тачно 11 пута. Сада ћемо одредити колико времена прође између два међусобно најближа поклапања. Због брзина кретања казаљки растојање између сатне и минутне казаљке представља у сваком моменту једанаест дванаестина од пута који је прешла минутна казаљка. У тренутку поклапања та разлика представља пун круг, односно 60 минутних подељака. Ако је m- број минута који протекну од 12 часова до првог следећег поклапања, онда је .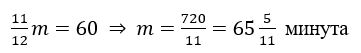

То смо и показали на сату који смо направили у GeoGebri.

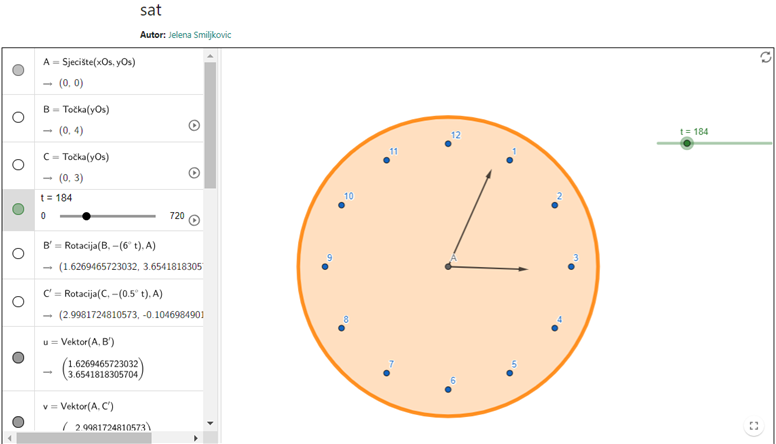
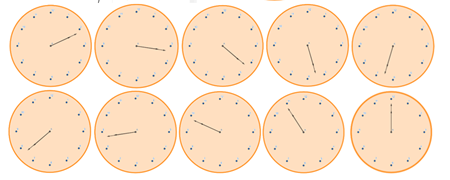
Колико пута у току 12 часова неко жели да нас загрли?

Када казаљке граде опружен угао верује се да нам следи загрљај, тако да ћемо се бавити и проблематиком колико пута у току дана неко жели да нас загрли користећи математичке прорачуне. Решење ћемо наћи користећи се закључцима о брзинама кретања казаљки из претходног задатка. Први пут после 12 часова казаљке ће заузети тражени положај када минутна казаљка престигне сатну за тачно тридесет минута. Нека се то догодило m минута после 12 часова.

Закључујемо да ће у току 12 часова казаљке 11 пута заузети положај опруженог угла. Проверићемо на сату који смо направили у GeoGebri.

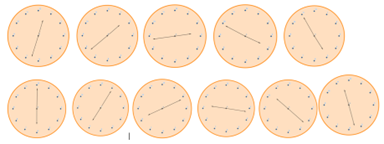
Радили смо занимљив задатак са ПИСА тестирања који лепо осликава проблем временских зона.

Задатак се зове разговор преко интернета и гласи: Марк из Сиднеја у Аустралији и Ханс из Берлина у Немачкој често међусобно комуницирају користећи „chat“ на Интернету. Да би могли да разговарају морају да се прикључе на Интернет у истом тренутку. Тражећи одговарајуће време за „chat“, Марк је консултовао карту временских зона и нашао следеће:

Питање 1: Када је 19h у Сиднеју, које време је у Берлину?

Одговор 1: 10 h ујутру.

Питање 2: Марк и Ханс не могу да разговарају између 9h и 16:30h по њиховим локалним временима, зато што морају да иду у школу. Исто тако, неће моћи да разговарају између 23h и 7h зато што ће тада да спавају. Када Марк и Ханс могу да разговарају? Упиши локално време у табелу.

Одговор 2: Сви временски интервали који уважавају временски помак од 9h, а у оквиру следећих интервала.

Сиднеј-16:30h-18:00h Берлин- 7:30h- 9:00h

или

Сиднеј- 7:00h- 8:00h Берлин- 22:30h- 23:00h

Сиднеј 17:00h Берлин 8:00h

Литерарни радови ученика инспирисани пројектом

Инспирисани пројектом ученици су кроз стихове исказали своје виђење времена и сата.

Закључак:

Кроз игру, истраживање и тимски рад реализовали смо пројекат. Упознали смо се са занимљивом страном математике и употребом нових технологија и алата у настави математике. Савладали смо конструкције правилних многоуглова. Усвојили појам Архимедовог тела- ромбикосидодекаедра и направили 3D-модел сата. Креирали сат у Геогебри. Реализовали смо радионицу рада са сламчицама. Истраживали о временским зонама и занимљивостима у вези градова и држава сваке временске зоне. Бавили смо се писањем литерарних радова. Истраживали смо о сатовима. Користили Геогебру и Волфрам алфу, 3Д бојанку, PicsArt и QR Kôd.

Забавили смо се и уочили да је математика свуда око нас. У плану је да направимо макету сата од чвршћег материјала који ће стајати у холу школе.

Ученици су мотивисани за учење кроз пројекте, истраживање и употребу ИКТ-а у настави. Колеге су заинтересоване за решавање проблема кроз међупредметну корелацију.

На нивоу сваког од 4 одељења којима предајем ове године покренут је по један пројекат који ће бити реализован у првом полугодишту. Ученици су одушевљени и пуни идеја.

Конкурс Сазнали на семинару применили у пракси 2019

Конкурс Сазнали на семинару применили у пракси 2019

Пријава на конкурс:

ПРОЈЕКАТ САТ

Опис пројекта

Тема пројекта је Сат. У складу са темом у наставку је представљен планиран начин реализације пројекта.

Циљ пројекта:

Исходи:

Ученик ће бити у стању да:

препозна и опише разлику између различитих типова сатова

препозна и опише разлику између временских зона

користи информационе технологије у решавању проблема

креира сат у Геогебри

нацрта мрежу ромбикосидодекаедра у Геогебри

истражи кроз Wolfram alpha изглед ромбикосидодекаедра

креира слике у PicsArt-у

направи QR Kôd

селектује битне информације

конструише правилне многоуглове

максимално искористи расположиви материјал за рад

креира прегледну ППТ

повеже тему са другим предметима и да сагледа ширу слику у оквиру просторно- временског контекста;

успешно сарађује са наставницима, ученицима и локалном заједницом.

саслуша и уважи туђе мишљење

аргументовано брани свој став

План пројекта

Пројекат се реализује у другом полугодишту, у месецу марту, априлу и мају, оквирно два час недељно.

недеља: Анализа задатог проблема и одређивање циља пројекта.

4. до 8. недеље: Рад на реализацији пројекта, прикупљање потребних информација и анализа истих од стране ученика уз консултацију са наставником.

9. и недеља: Креирање крајњег продукт рада.

11. недеља: Презентовање резултата рада.

недеља: Оцењивање и вредновање резултата у сарадњи ученика и наставника.

Активности ученика и наставника, начини презентовања пројекта

Активности наставника:

Предлаже циљ и тему пројекта.

Формира групе у сарадњи са ученицима.

Прати, пружа подршку и усмерава ученике у раду.

Подстиче ученике на стваралачко истраживање.

Подстиче сарадњу и тимски рад међу ученицима.

Помаже ученицима у превазилажењу тешкоћа и савладавању проблема.

Заједно са ученицима вреднује резултате.

Пружа помоћ при остваривању видљивости резултата пројекта.

Подстиче ученике да изкажу своје мишљење и ставове.

Подстиче ученике да вежбају јавни наступ.

Помаже ученицима да уоче да је математика свуда око нас.

Активности ученика:

Планирају фазе и ток реализације;

Прикупљају информације, материјале, врше анализу;

Креирају крајњи продукт;

Презентују резултате;

Учествују у вредновању резултата.

Праћење и вредновање пројекта

Дискусија

Рефлексија

Евалуација

Скала процене из угла ученика:

Наставничка евалуација

Наставник је креирао сопствену табелу за праћење и вредновање процеса на индивидуалном и групном нивоу. Утиске и процену ће поделити са ученицима по завршетку.

Скала процене из угла наставника (описно):

Разрада пројекта

Први сатови

Сат са клатном

Временске зоне

Математички појмови и софтверски алати

Wolfram alpha – детаљни опис ромбикосидодекаедра

rhombicosidodecahedron, minimal edge length = 5

https://www.wolframalpha.com/input/?i=rhombicosidodecahedron,+minimal+edge+length+%3D+9

Geogebra – мрежа ромбикосидодекаедра са задатим параметрима

Geogebra android – Мобилна апликација

Коришћење Геогебра мобилне апликације за једноставно дефинисање геометријских фигура и обнављање градива.

3D бојанка- приказ мреже ромбикосидодекаедра са налепницама сатова

Етапе израде макете и радионица- прављење ромбикосидодекаедра од сламчица

Организована је и радионица на којој је направљен ромбикосидодекаедар од сламчица.

Задаци у вези сата:

Колико пута у току 12 часова неко мисли на нас?

Од давнина се верује да неко мисли на нас када су казаљке поклопљене. Тим проблемом бавили смо се у овом пројекту и до тачног одговора дошли смо математичким путем.

То смо и показали на сату који смо направили у GeoGebri.

Закључујемо да ће у току 12 часова казаљке 11 пута заузети положај опруженог угла. Проверићемо на сату који смо направили у GeoGebri.

Питање 1: Када је 19h у Сиднеју, које време је у Берлину?

Одговор 1: 10 h ујутру.